A LÓGICA DA LOUCURA EM "ALICE NO PAÍS DOS ENIGMAS" DE SMULLYAN

Abstract

A LÓGICA DA LOUCURA EM “ALICE NO PAÍS DOS ENIGMAS” DE SMULLYAN

BOLSISTA: LUAN PAULO PEREIRA¹, ORIENTADOR: NEWTON MARQUES PERON²

¹Graduado em Filosofia pela UFFS. Graduando em Matemática pela UFFS.

E-mail: luanpaulopereira@hotmail.com

²Professor do Curso de Filosofia da UFFS. E-mail: newton.peron@uffs.edu.br

1 Introdução

Puzzles lógicos atualmente são encontrados em muitos lugares, partindo de bancas de jornais a aplicativos para smartphones. Dentre os mais diversos tipos de puzzles, ressaltamos o trabalho do renomado lógico e matemático estadunidense Raymond Smullyan. Além de possuir em sua bibliografia uma vasta coleção de livros sobre lógica formal, possui vários livros de puzzles matemáticos e lógicos. Com relação aos puzzles, foram traduzidos para o português os seguintes livros: “Alice no país dos enigmas”, “Os enigmas de Sherazade” e “A dama ou o tigre?”.

Dentro dos livros descritos acima, focaremos somente no capítulo 3 de “Alice no País dos Enigmas”. Neste livro, é baseado em dois clássicos da literatura universal: “Alice no País das Maravilhas” e Alice no País dos Enigmas”. Partindo das aventuras da personagem Alice, Smullyan lança uma série de problemas lógicos, jogos com números, meta-enigmas, exercícios de verdade/mentira, charadas e paradoxos.

2 Objetivos

Nossa pesquisa consiste em fazer um recorte do livro “Alice no País dos Enigmas”, ao selecionar somente o capítulo 3 deste livro para uma análise. Em seguida, esses puzzles foram comentados e formalizados. Mas para fazer isso foi necessário desenvolver uma Lógica da Loucura, uma extensão do CPC (Cálculo Proposicional Clássico).

A Lógica da Loucura foi inspirada nos operadores epistêmicos de Jaakko Hintikka. Sua concepção, em uma linguagem formal, a fórmula B_cα significa em linguagem natural que o agente c acredita (em inglês, believe), na sentença α. O nosso único acréscimo foi o predicado L. Mas para construí-la, se faz necessário apresentar regras para a sua linguagem. Para isso, adaptado da capítulo 6 de (Mortari, 2001), desenvolvemos o seu alfabeto e as cláusulas para construção de fórmulas. Assim, temos o conhecimento necessário para formalizar as premissas do puzzle.

Sendo um dos objetivos a formalização do raciocínio de como os puzzles foram resolvidos, apresentamos a regras para dedução natural. Para tanto, adaptamos dos capítulos 14 e 15de (Mortari,2001). Mas as regras apresentadas nesses capítulos, não é suficiente para formalizar estes enigmas. Partindo do diálogo entre Alice e Duquesa, personagens de “Alice no País dos Enigmas”, acrescentamos a seguinte regra, denominada Regra da Loucura I (RL1):

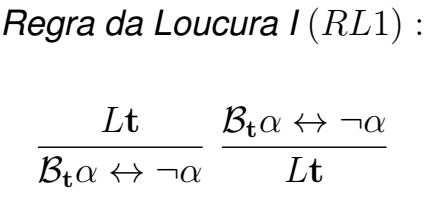
Esta regra foi inspirada na Lógica da Mentira proposta por Adam Kolany em (Kolani,1996). Nessa lógica, T a é lido como o indivíduo a é um true-teller, ou seja, um indivíduo que só diz a verdade. Já a fórmula a►α significa que o indivíduo a disse a fórmula α. A Lógica da Mentira pode ser obtida acrescentando ao Cálculo Proposicional Clássico a seguinte regra:

Esta formulação não é idêntica à lógica da mentira de Kolany, mas pode-se demonstrar que são equivalentes.

3 Metodologia

A metodologia aplicada foi puramente bibliográfica.

4 Resultados

Com esta pesquisa, conseguimos formalizar, através da Lógica da Loucura, as premissas e a resolução dos puzzles presentes no capítulo 3 de “Alice no País dos Enigmas”.

4 Conclusão

O desenvolvimento da presente pesquisa mostrou não apenas como formalizar alguns
puzzles de Raymond Smullyan. Como a Lógica da Loucura pode ser adaptada para o
contexto do Paradoxo de Epimênides, acreditamos que essa lógica pode ser usada nas
mais variadas situações. Além disso, ao formalizar o puzzle e o raciocínio do autor, se
permitiu analisar as diferenças entre a linguagem natural e linguagem formal.

Este trabalho não se propõe esgotar o tema. Ao contrário, temos a pretensão de mos
trar o quanto ainda pode ser feito com os capítulos restantes de “Alice no País dos Enig
mas”. Esperamos que este trabalho seja o começo de muitos.

Claramente, não temos nenhuma garantia que as regras e definições apresentadas
são de fatos consistentes. Poderíamos a chegar a uma contradição. Para isso, se faz
necessário uma semântica para a Lógica da Loucura. Poderíamos ainda estabelecer uma
combinação da Lógica da Loucura com a Lógica da Mentira nos puzzles de Smullyan. Mas esta tarefa será deixada para um futuro trabalho.

5 Referências

[CARNIELLI; EPSTEIN, 2005] CARNIELLI, W.; EPSTEIN, R. Computabilidade, Funções Computáveis, Lógica e os Fundamentos da Matemática. Editora Unesp, São Paulo, SP, 2005

[CARROLL, 2018] CARROLL, L.. Alice: edição comentada e ilustrada. Jorge Zahar, Rio de Janeiro, RJ, 2000.

[HENDRICKS;SYMONS, 2018] HENDRICKS, V.; SYMONS J. Epistemic Logic. In Zalta, E. N., editor, The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University, 2015. Disponível em
<https://plato.stanford.edu/entries/logic-epistemic/>. Acesso em: 2 jun. 2018.

[KOLANI, 1996] KOLANI, A. A General Method of Solving Smullyan’s puzzles. Logic and Logical Philosophy, 4:97–103, 1996.

[MORTARI, 2001] MORTARI, C. A. Introdução à Lógica. Editora Unesp, São Paulo, 2001.

[SMULLYAN, 2000] SMULLYAN, R. Alice no País dos Enigmas. Jorge Zahar, Rio de
Janeiro, RJ, 2000.

6 Palavras-chave: Lógica da Loucura – Smullyan – Formalização – Puzzle

7 Financiamento:

Fapesc / UFFS